This article provides a comprehensive discussion of the chi-square test of independence, the assumptions, and a step-by-step procedure on how to run the chi-square test in SPSS.
Definition: What is a Chi-Square Test of Independence?
A chi-square test of independence is a non-parametric statistical test that is widely used in research to determine whether there is an association between categorical variables. The chi-square test of independence is also called a chi-square test of Association. Thus, by performing a chi-square test of independence in SPSS, you can be able to determine whether there is an association between any two categorical variables.
You can learn more about non-parametric tests in our article: Difference between parametric and non-parametric tests
Chi-Square Test of Independence Example
Consider a scenario where you wish to determine whether there is an association between education level (primary, secondary, and tertiary) and Employment status (Unemployed, Employed). In this case, performing a chi-square test of independence can allow you to determine whether there is a relationship between education level and employment status.
Chi-Square Test of Independence Assumptions
Before deciding to use a chi-square test of independence in your research, you need to make sure that your data meets the two main assumptions of a chi-square test of independence. Testing these assumptions is mainly important because it allows you to validate why you performed a chi-square test of independence and not the chi-square goodness of fit. If these assumptions are not met, then conducting a chi-square test of independence will yield inaccurate and unreliable results.
The two main assumptions are:
- Categorical Variables – The two variables should be categorical. This means they should be measured using either a nominal or ordinal level of measurement.
- Each Categorical Variable should have two or more independent categories – For instance, if you want to test where there is an association between gender and employment status, then these variables meet this assumption because: Gender has two categories (Male/Female), and Employment status (Not-employed/Employed).
Test Procedure for Performing a Chi-Square Test in SPSS [Chi-square test of independence]
Follow these 6 simple steps to run a chi-square test of independence (Association) in SPSS
- Step 1: Click Analyze > Descriptives Statistics > Crosstabs as shown below

- Step 2: Move one of the categorical variables into the Row(s): box and the other categorical variable into the Column(s): box. as shown below.

- Step 3: Click on the Statistics Button and Select the Chi-square and Phi and Cramer’s V options, as shown below: The Chi-square will output the chi-square test of independence value, while the Phi and Cramer’s V will output the Effect Size of the chi-square test of independence.
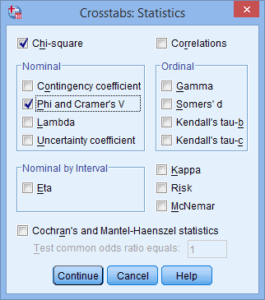
- Step 4: Click Continue
- Step 5: Click the Cells Button and Select Observed from the –Counts Section. Also, from the Percentages Section, Select Row, Column, and Total, as shown below:

- Step 6: Click the Continue Button and Then, the OK button to generate the chi-square test of independence Results.
Struggling with calculating a chi-square test of independence by hand? Learn more about the chi-square test of independence from our article on: mastering the chi-square test of independence.