interpreting and reporting Pearson's correlation spss outputs

How to Interpret and Report Pearson’s Correlation SPSS Outputs

Have you ever performed a correlation analysis in SPSS, but struggled to make sense of the output? Perhaps you’re unsure how to interpret the correlation coefficient itself, or maybe you’re wondering how to report your findings in APA style. This guide is designed to bridge that gap. We’ll equip you with the skills to confidently interpret and report Pearson’s correlation SPSS outputs. So, by the end of this tutorial, you’ll gain a comprehensive understanding of how to interpret correlation analysis SPSS outputs correctly. Specifically, you will learn how to interpret the strength and direction of the relationship, evaluating statistical significance, and crafting clear report using APA style.

What is Pearson’s Correlation?

Pearson’s correlation, usually denoted by a Greek letter “ρ”, or “r” is a statistical test that measures the strength and direction of a linear relationship between two continuous variables. Let’s consider a scenario where you’ve plotted your data using a Scatter Plot and the points tends to form a straight diagonal line (either upwards, or downwards). In such a case, it is worth to run a Pearson’s correlation analysis to quantify the strength of the linear relationship.

It is worth noting that:

  • A positive correlation (r between 0 and 1) indicates that as the value of one variable increases, the other variable tends to increase as well.
  • A negative correlation (r between -1 and 0) means that as one variable goes up, the other tends to go down.
  • A correlation close to zero suggests little to no linear relationship between the variables.

NOTE: Correlation value does not imply causation! Just because two things are correlated doesn’t mean one variable causes the other. There might be a third unseen factor influencing both variables.

Assumptions of Pearson’s Correlation

While Pearson’s correlation is a powerful statistical test, its reliability and validity depends on several assumptions: Some of these assumptions include:

  1. Continuous Variables: The two variables under investigation must be measured on a continuous scale (either interval or ratio measure). Some examples of continuous variables include; height, weight, or exam scores.
  2. Linear Relationship: The correlation coefficient measures the strength of a linear relationship between two variables. This means that it is not ideal for non-linear relationships.
  3. Normally Distributed Data: Ideally, the data for both variables should be approximately normally distributed.

If your data doesn’t meet these assumptions, alternative correlation measures such as Spearman’s Correlation might be more suitable.

Recall: Checking these assumptions before interpreting your Pearson’s correlation results ensures you’re drawing reliable conclusions from your data.

How to Interpret and Report Pearson’s Correlation SPSS Outputs

Now that you’ve learnt how to run the Pearson’s correlation analysis in SPSS (refer to this guide for example used and how to perform the test using SPSS) in our previous guide, let’s dive into interpreting the Pearson’s Correlation SPSS outputs.

Here are the SPSS Outputs from our how to run Pearson’s correlation using SPSS.

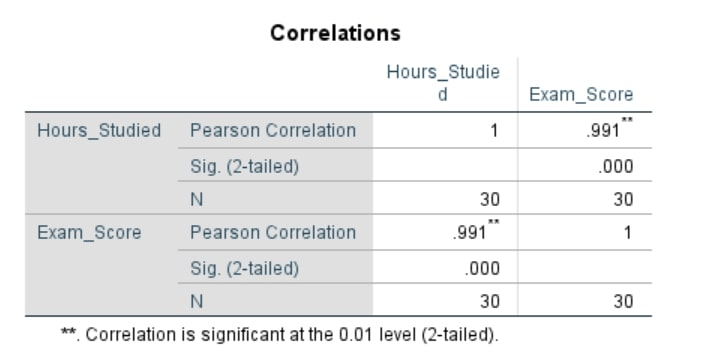
Pearson's correlation SPSS outputs

Based on the above outputs;

  • Pearson Correlation: The correlation coefficient (r) between hours studied and exam scores is .991, which is very close to 1. This indicates that there was a very strong positive relationship between these two variables.
  • Significance (2-tailed): The p-value is .000, which is less than .001. This indicates that the correlation is statistically significant at the 0.01 level of significance.
  • N: The sample size (n) is 30 for both variables.

Reporting Pearson’s Correlation SPSS Outputs in APA Style

If you want to report the above Pearson’s correlation SPSS Outputs in APA Style, then you can imitate this style;

A Pearson correlation analysis was conducted to examine the relationship between the number of hours studied per week and the final exam scores among university students. The results indicated a very strong, positive, and significant correlation between hours studied and exam scores, r(28)=.991, p<.001. This result indicates that as the number of hours studied per week increases, the final exam scores also tend to increase significantly. In other words, the finding suggests that higher numbers of study hours are associated with higher exam scores.

Related Posts