![Binomial Probability Calculator [Exact & cumulative probabilities]](https://online-spss.com/wp-content/uploads/2025/03/Binomial-distribution-probability-calculator.jpg)
The binomial distribution is a probability distribution that describes the likelihood of a certain number of successes in a fixed number of trials. Each trial has only two possible outcomes: success or failure. This distribution is widely used in statistics and probability to model real-life situations, such as predicting the number of defective products in a batch or the chances of passing a test based on multiple-choice questions. To simplify these calculations, our Binomial Probability Calculator provides quick and accurate results. It helps users compute exact and cumulative probabilities without manually using complex formulas.
What is Binomial Distribution?
The binomial distribution is a type of probability distribution that describes the number of times an event happens in a fixed number of trials. Each trial has only two possible outcomes: success or failure.
For an experiment to follow a binomial distribution, it must meet these conditions:
- There is a fixed number of trials (n).
- Each trial has only two possible outcomes (Success or Failure).
- The probability of success (p) remains the same in every trial.
- Each trial is independent, meaning the result of one trial does not affect another.
Real-Life Examples:
- Flipping a coin multiple times and counting how many times it lands on heads.
- Checking defective products in a batch of items.
- Survey responses, where people either agree (success) or disagree (failure).
- Medical trials, such as testing if a new drug works on a set number of patients.
The binomial distribution is useful in predicting probabilities in these and many other situations.
Binomial Probability Formula
The binomial probability formula calculates the probability of getting exactly x successes in n independent trials. The formula for the binomial probability is as follows:
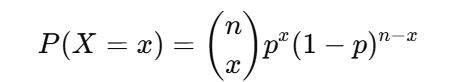
Where:
- P (X=x) is the probability of getting exactly xxx successes
- n is the total number of trials
- x is the desired number of successes
- p is the probability of success in each trial
- 1−p is the probability of failure in each trial
Example Calculation
Problem: A fair coin is flipped 5 times. What is the probability of getting exactly 3 heads?
Step 1: Identify the values
- n=5 (total flips)
- x=3 (desired heads)
- p=0.5 (probability of heads in each flip for a fair coin)
Step 2: Apply the formula
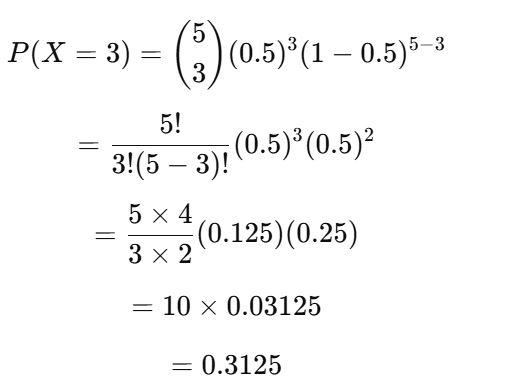
So, the probability of getting exactly 3 heads in 5 flips of a fair coin is 0.3125 (31.25%).
How to Use the Binomial Probability Calculator
Our Binomial Distribution Probability Calculator makes it easy to compute probabilities for binomial experiments. Follow these simple steps to use it:
Step 1: Enter the required values
- Number of trials (n) – The total number of times the experiment is repeated.
- Probability of success (p) – The likelihood of success in each trial.
- Number of successes (x) – The specific number of times success is expected.
Step 2: Select the Probability Output
The calculator provides different types of probabilities:
- P(X=x): (Exact Probability) – This gives the probability of getting exactly x successes in n trials.
- P(X<x): (Cumulative Probability Less Than x) – This calculates the probability of getting fewer than x successes.
- P(X≤x): (Cumulative Probability Up to x) – This finds the probability of getting x or fewer successes.
- P(X>x): (Probability of More Than x Successes) – This determines the chance of getting more than x successes.
- P(X≥x): (Probability of At Least x Successes) – This gives the probability of getting x or more successes.
Therefore, with our binomial probability calculator, you can quickly analyze binomial probabilities for real-world applications, such as predicting product defects, survey results, or medical study outcomes.
Try the Binomial Distribution Probability Calculator Now
Use our Binomial Probability Calculator to quickly find probabilities for binomial experiments. Simply
Binomial Probability Calculator
- Enter the number of trials (n), the probability of success (p), and the desired number of successes (x).
- Click the Calculate button to compute binomial and cumulative probabilities.
Results
- Exact Probability: P(X = x):
- Cumulative Probability Less Than x successes: P(X < x):
- Cumulative Probability of at most x successes: P(X ≤ x):
- Cumulative Probability of More Than x Successes: P(X > x):
- Cumulative Probability of At Least x Successes: P(X ≥ x):
Frequently Asked Questions
A binomial experiment is a statistical experiment that meets the following conditions:
- It consists of a fixed number of trials (n).
- Each trial has only two possible outcomes (success or failure).
- The probability of success remains constant across all trials.
- Each trial is independent of the others.
A binomial distribution is a probability distribution that models the number of successes in a binomial experiment. It describes how likely different numbers of successes are, given a set number of trials and a fixed probability of success.
The number of trials (n) is the total number of times an experiment is repeated. For example, if you flip a coin 10 times, then the number of trials is 10.
The number of successes (x) is the specific number of times the desired outcome occurs in the trials. For example, if you flip a coin 10 times and get 6 heads, then the number of successes is 6 (if "heads" is considered a success).
The probability of success (p) is the likelihood that the desired outcome happens in one trial. For example, if a coin is fair, the probability of getting heads is 0.5 (50%).
Struggling with Binomial Probability?
We’re Here to Help! Binomial probability calculations can be tricky, especially when dealing with large datasets or complex problems. If you're unsure how to apply the formulas or interpret the results, our expert statisticians are ready to assist you!
Don't let binomial probability slow you down! Contact us today for professional statistics help and make your data analysis effortless.
